當(dāng)前位置: CompoTech China > 關(guān)鍵技術(shù)和應(yīng)用 >
摘要
本文介紹如何使用降階隆伯格觀測(cè)器(ROLO)估算永磁同步電機(jī)(PMSM)的轉(zhuǎn)子磁鏈位置。首先介紹特征值與穩(wěn)定性的關(guān)系;在此基礎(chǔ)上,引入狀態(tài)反饋控制的理念;接著介紹如何使用該理念來設(shè)計(jì)隆伯格觀測(cè)器;然后,以PMSM為例,推導(dǎo)ROLO的設(shè)計(jì)過程,給出設(shè)計(jì)結(jié)果;最后,介紹Microchip的相關(guān)電機(jī)控制方案(評(píng)估套件、例程和文檔等)。
關(guān)鍵詞
降階隆伯格觀測(cè)器,永磁同步電機(jī),反電動(dòng)勢(shì)估算,MPLAB® Harmony 3
概述
永磁同步電機(jī)(PMSM)的磁場定向控制(FOC)在近十幾年成為了主流的電機(jī)控制方法。其中,無位置傳感器FOC由于其低成本和高可靠性,獲得了越來越多的應(yīng)用和關(guān)注。由于沒有位置傳感器,所以必須估算轉(zhuǎn)子磁鏈位置。由于在旋轉(zhuǎn)過程中,轉(zhuǎn)子磁鏈生成反電動(dòng)勢(shì)(BEMF),并且BEMF超前轉(zhuǎn)子磁鏈π/2弧度,所以可以利用對(duì)BEMF進(jìn)行觀測(cè),進(jìn)而估算轉(zhuǎn)子磁鏈。降階隆伯格觀測(cè)器(ROLO)是一種常用的BEMF觀測(cè)手段。
一方面,工程師可能不具備設(shè)計(jì)觀測(cè)器所需的背景知識(shí);另一方面,產(chǎn)品開發(fā)項(xiàng)目必須盡快且高質(zhì)量地完成。盡管可以找到背景知識(shí)的相關(guān)教材,但由于其缺少針對(duì)性,所以工程師不得不花費(fèi)大量時(shí)間進(jìn)行學(xué)習(xí)。該矛盾經(jīng)常成為制約產(chǎn)品開發(fā)進(jìn)度和質(zhì)量的瓶頸。針對(duì)此困境,ROLO由于其原理簡單,成為了能短時(shí)間掌握的優(yōu)選方案。
本文針對(duì)PMSM控制所需,篩選出最少量的必需知識(shí),按照邏輯順序闡述利用ROLO觀測(cè)BEMF的原理。此外,還介紹了Microchip的相關(guān)電機(jī)控制方案。讀者可以借此快速掌握原理,并且上手實(shí)踐和熟悉。
特征值與穩(wěn)定性
常微分方程(ODE)是時(shí)間確定性系統(tǒng)的一種抽象模型。PMSM可以看作是一個(gè)線性時(shí)間確定性系統(tǒng),因此可以用線性常微分方程來建模。
考慮以下的一般線性O(shè)DE:
其中,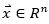 是隨時(shí)間t變化的狀態(tài)向量。
是隨時(shí)間t變化的狀態(tài)向量。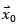 是0時(shí)刻的初始狀態(tài)。
是0時(shí)刻的初始狀態(tài)。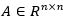 是一個(gè)已知方陣。我們關(guān)心的是,
是一個(gè)已知方陣。我們關(guān)心的是,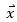 是否趨向于
是否趨向于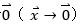 ?
?
假設(shè)A擁有n個(gè)相互獨(dú)立的特征向量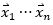 ,對(duì)應(yīng)的特征值是
,對(duì)應(yīng)的特征值是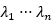 。那么可以把A分解為:
。那么可以把A分解為:
其中,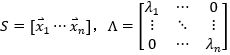 。
。
由于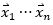 是空間
是空間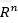 的一組基,所以任意
的一組基,所以任意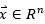 都可以表示為
都可以表示為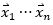 的線性組合:
的線性組合:
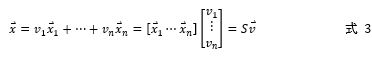
把式3代入式1,得到:
于是:
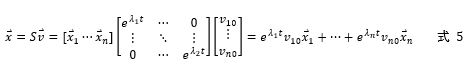
從式 5可以看出,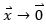 當(dāng)且僅當(dāng)A的所有特征值
當(dāng)且僅當(dāng)A的所有特征值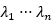 都位于復(fù)平面的左半面。
都位于復(fù)平面的左半面。
狀態(tài)反饋控制
假設(shè)式 1是某個(gè)物理系統(tǒng)的ODE模型。顯然,矩陣A是由物理系統(tǒng)客觀決定的。因此,系統(tǒng)狀態(tài)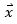 不一定→
不一定→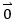 。對(duì)該系統(tǒng),我們可以施加一個(gè)輸入向量
。對(duì)該系統(tǒng),我們可以施加一個(gè)輸入向量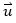 :
:
其中,B是由物理系統(tǒng)決定的已知矩陣。能否通過選擇合適的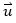 使得
使得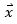 一定→
一定→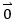 ?答案是肯定的。一個(gè)簡單的選擇是狀態(tài)反饋比例控制:
?答案是肯定的。一個(gè)簡單的選擇是狀態(tài)反饋比例控制:
其中,K是比例增益。于是,式 6變?yōu)椋?/span>
只要選擇合適的K,使A-BK的所有特征值都位于復(fù)平面的左半面,就可以確保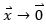 。
。
隆伯格觀測(cè)器
考慮以下系統(tǒng):
其中,C是由物理系統(tǒng)決定的已知矩陣,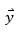 是輸出向量,并且
是輸出向量,并且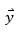 可以直接測(cè)得,
可以直接測(cè)得,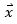 不能直接測(cè)得。能否利用已知信息A,B,C,
不能直接測(cè)得。能否利用已知信息A,B,C,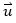 ,
,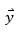 來估算
來估算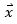 ?
?
我們首先嘗試做開環(huán)仿真估算:
其中,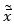 是
是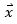 的估算值。把式 9與式 10相減,可以檢驗(yàn)估算效果:
的估算值。把式 9與式 10相減,可以檢驗(yàn)估算效果:
其中,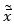 =
=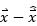 是估算誤差。顯然,
是估算誤差。顯然,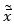 不一定→
不一定→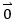 。但注意到式 11與式 1的形式完全相同,因此應(yīng)當(dāng)考慮使用類似于式 7那樣的狀態(tài)反饋控制來使
。但注意到式 11與式 1的形式完全相同,因此應(yīng)當(dāng)考慮使用類似于式 7那樣的狀態(tài)反饋控制來使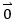 →
→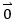 。
。
由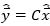 可得:
可得: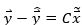 。其中,
。其中,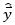 是
是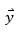 的估算值。
的估算值。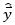 和
和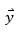 都是已知的,于是
都是已知的,于是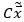 ,即系統(tǒng)式 11的狀態(tài)反饋信息,也是已知的。我們只需要對(duì)系統(tǒng)式 11施加狀態(tài)反饋控制,使系統(tǒng)模型變?yōu)椋?/span>
,即系統(tǒng)式 11的狀態(tài)反饋信息,也是已知的。我們只需要對(duì)系統(tǒng)式 11施加狀態(tài)反饋控制,使系統(tǒng)模型變?yōu)椋?/span>
并且選擇合適的矩陣L,使A-LC的所有特征值都位于復(fù)平面的左半面,就可以確保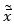 →
→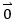 。
。
為了實(shí)現(xiàn)式 12,必須設(shè)計(jì)如下的觀測(cè)器:
式 13由斯坦福大學(xué)的大衛(wèi).隆伯格教授提出,因此命名為隆伯格觀測(cè)器。
觀測(cè)PMSM的BEMF
在靜止兩相坐標(biāo)系(α-β坐標(biāo)系)中,表貼式PMSM的電壓方程為:
其中,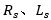 是定子線圈相電阻、相電感;u、i、e是在α軸或β軸上的電壓、電流、反電動(dòng)勢(shì)。反電動(dòng)勢(shì)是由轉(zhuǎn)子磁鏈旋轉(zhuǎn)而生成的,因而受制于以下ODE:
是定子線圈相電阻、相電感;u、i、e是在α軸或β軸上的電壓、電流、反電動(dòng)勢(shì)。反電動(dòng)勢(shì)是由轉(zhuǎn)子磁鏈旋轉(zhuǎn)而生成的,因而受制于以下ODE:
其中,ω是電氣轉(zhuǎn)速。
把式 14和式 15寫成矩陣形式,即表貼式PMSM在α-β坐標(biāo)系中的ODE模型:
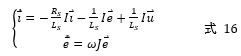
其中,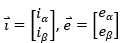 是系統(tǒng)狀態(tài)向量;
是系統(tǒng)狀態(tài)向量;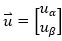 是輸入向量;
是輸入向量;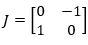 。
。
由于i ?可以通過傳感器采集到,因此可以把它看作已知量,而不是系統(tǒng)狀態(tài)。基于這種觀點(diǎn),系統(tǒng)的階數(shù)由原來的4降低為2。相應(yīng)地,式 16的形式變?yōu)椋?/span>
應(yīng)當(dāng)注意到,式 17與式 9的形式一致。讀者能輕易地看出他們之間的對(duì)應(yīng)關(guān)系。于是,只要根據(jù)式 13就可以直接設(shè)計(jì)出針對(duì)e ?的隆伯格觀測(cè)器。對(duì)此,本文不做展開,并鼓勵(lì)讀者親自進(jìn)行推導(dǎo)。需要指出的是,這樣的觀測(cè)器被稱為降階隆伯格觀測(cè)器。
Microchip的ROLO方案
Microchip的基于ROLO的PMSM無傳感器控制方案提供例程、評(píng)估套件、開發(fā)工具和幫助文檔。
例程位于MPLAB® Harmony 3的motor control模塊中,是一個(gè)運(yùn)行在Cortex®-M0+ MCU(SAMC21)之上的MPLAB X工程:pmsm_foc_rolo_sam_c21。
該演示方案可以運(yùn)行于MCLV2低壓電機(jī)控制評(píng)估套件或MCHV3高壓電機(jī)控制評(píng)估套件。兩款評(píng)估套件均可在Microchip官網(wǎng)搜索并訂購。
該例程利用圖形化配置工具M(jìn)PLAB Harmony配置器(MHC)生成。使用MPLAB X IDE打開該工程,并打開MHC,就可以看到CPU和所需片上周邊(PWM模塊和ADC等)的配置情況,如圖 1 所示。
相應(yīng)的幫助文檔也位于MPLAB Harmony 3的motor control模塊中。其中介紹了如何搭建硬件平臺(tái)、編譯和下載工程、算法原理框圖、軟件流程圖、軟件配置方法等,如圖 2、圖 3、 圖 4和圖 5 所示。
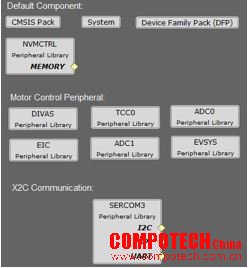
< 圖 1. 例程的MHC配置 >
< 圖 2. 電機(jī)控制算法框圖 >
< 圖 3. 軟件流程圖 >
< 圖 4. 軟件配置方法:電機(jī)參數(shù)宏定義列表 >

< 圖 5. 低壓電機(jī)控制硬件連接 >
總結(jié)
本文從PMSM的ODE模型開始,逐步介紹了基于ROLO的BEMF觀測(cè)器的設(shè)計(jì)理念和方法;并且介紹了Microchip的相關(guān)方案。讀者可以利用這些資源快速掌握原理并上手實(shí)踐、熟悉PMSM的無傳感器控制方法,以加快項(xiàng)目開發(fā)進(jìn)度和提升產(chǎn)品性能。
八、 參考文獻(xiàn)
1. AN2590, Sensorless FOC for PMSM Using Reduced Order Luenberger Observer, Microchip Technology. (https://ww1.microchip.com/downloads/en/AppNotes/00002590B.pdf)
2. MPLAB Harmony 3: motor control module.
3. Microchip工程師社區(qū)知識(shí)庫:《Harmony 3電機(jī)控制資源初探》(http://www.microchip.com.cn/newcommunity//Uploads/H3_Chinese_guides/guide-17.pdf)
本月熱點(diǎn) HOME
- 使用熱插拔控制器增強(qiáng)系統(tǒng)可
- IP Your Way——您提供規(guī)格,然后
- 設(shè)計(jì)更安全、更智能、互聯(lián)程
- 使用合適的窗口電壓監(jiān)控器優(yōu)
- 區(qū)域架構(gòu)如何為完全由軟件定
- 汽車 GPU 算力新高度支持智駕芯
- 無輔助繞組 GaN 反激式轉(zhuǎn)換器如
- 帶硬件同步功能的以太網(wǎng) PHY
- 采用創(chuàng)新型 C29 內(nèi)核的 MCU 如何
- 在校準(zhǔn)中使用埋入式齊納技術(shù)
- 人工智能對(duì)數(shù)據(jù)中心基礎(chǔ)設(shè)施
- 軟件定義車輛改變汽車行業(yè)的
欄目熱點(diǎn) HOME
- 業(yè)界資訊
 是德科技 FieldFox 手持式分析儀配合 VDI 擴(kuò)頻模塊,實(shí)現(xiàn)毫米波分析功能
是德科技 FieldFox 手持式分析儀配合 VDI 擴(kuò)頻模塊,實(shí)現(xiàn)毫米波分析功能 -
業(yè)界資訊

ELARIS與泉州大學(xué)達(dá)成突破性合作,共同推廣智能駕駛技術(shù)
12-19 -
業(yè)界資訊

全球大賽再奪殊榮,晶泰科技 AI+量子物理技術(shù)再解行業(yè)難題
12-20 -
業(yè)界資訊

香港生產(chǎn)力促進(jìn)局2021年「成就智上」年度主題
02-28 -
業(yè)界資訊

黑芝麻智能發(fā)布華山A2000家族芯片平臺(tái),打造全場景通識(shí)智駕標(biāo)桿
12-31 -
業(yè)界資訊

黑芝麻智能發(fā)布華山A2000家族芯片平臺(tái),打造全場景通識(shí)智駕標(biāo)桿
12-31
